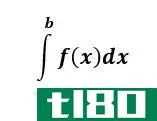第1部分第3部分：直接参数化

1. 1应用等值积分的黎曼和定义.定义。给定一个复数函数f(z){displaystyle f(z)}和一个轮廓γ,{displaystyle \gamma,}，f(z){displaystyle f(z)}在γ{displaystyle \gamma }上的积分被称为黎曼和limn→∞∑i=0nf（zi）Δzi。{displaystyle lim _{n\ to infty }\sum _{i=0}^{n}f(z_{i})\Delta z_{i}.}。如果这个极限存在，那么我们说f(z){displaystyle f(z)}在γ上是可整定的{displaystyle \gamma .}。我们通过写∫γf(z)dz.{displaystyle\int _{\gamma }f(z)mathrm {d} z.}来传达这一点，直观地说，这是一个非常直接的黎曼之和的概括。我们只是简单地将矩形相加来寻找曲线的面积，并将矩形的宽度送至0，从而使它们变得无限薄。
2. 2用参数t{\displaystyle t}重新写轮廓积分。如果我们将轮廓γ{displaystyle\gamma }参数化为z(t),{\displaystyle z(t),}，那么通过链规则，我们可以等效地写出以下积分。∫γf(z)dz=∫Δtf(z(t))dzdtdt{displaystyle int _{gamma }f(z)\mathrm {d} z=int _{Delta t}f(z(t)){frac {mathrm {d} z}{mathrm {d} t}\mathrm {d} t} 这就是我们用来计算的积分。一个重要的说明是，这个积分可以用它的实部和虚部来写，就像这样。∫Δtf(z(t))dzdtdt=∫Δt(u(t)+iv(t))dt{displaystyle {int _{Delta t}f(z(t)){frac {mathrm {d} z}{mathrm {d} t}}\mathrm {d} t=int _{Delta t}(u(t)+iv(t))\mathrm {d} t｝
3. 3参数化γ{displaystyle \gamma }并计算dzdt{frac {mathrm {d} z}{mathrm {d} t}}.在复杂分析中使用的最简单的轮廓线是线和圆的轮廓。为了简单起见，通常希望对一条线进行参数化，使0≤t≤1.{displaystyle 0\leq t\leq 1.}。给出一个起点z1{displaystyle z_{1}}和一个端点z2,{displaystyle z_{2},}这样的轮廓线一般可以用以下方式来参数化。z(t)=(1-t)z1+z2, 0≤t≤1{displaystyle z(t)=(1-t)z_{1}+z_{2},\ 0\leq t\leq 1}只要我们保持跟踪轮廓的方向，一个圆形轮廓也可以用一种简单的方式进行参数化。让z0{displaystyle z_{0}}是圆的中心，r{displaystyle r}是圆的半径。那么，从t=0,{displaystyle t=0,}开始并沿逆时针方向遍历轮廓的圆的参数化是这样的。z(t)=z0+reit, 0≤t≤2π{displaystyle z(t)=z_{0}+re^{it},\ 0\leq t\leq 2\pi }从这两条等高线计算dzdt{displaystyle {frac {mathrm {d} z}{mathrm {d} t}}}是很简单的。这里有两个重要事实需要考虑。首先，轮廓积分∫γf(z)dz{displaystyle\int _{\gamma }f(z)åmathrm {d} z}与参数化无关，只要γ{displaystyle\gamma }的方向保持不变。这意味着有无数种方法可以对给定的曲线进行参数化，因为速度可以以任意的方式变化。其次，扭转轮廓的方向会否定积分。∫-γf(z)dz=-∫γf(z)dz{{displaystyle int _{-\gamma }f(z)\mathrm {d} z=-int _{\gamma }f(z)\mathrm {d} z}。
4. 4评估。我们知道t{displaystyle t}是实值的，所以剩下的就是使用实变数微积分的标准积分技术进行积分。从点a{displaystyle a,}开始，等高线沿逆时针方向穿越半径为a{displaystyle a}的半圆，并以一条从-a{displaystyle -a}到a.{displaystyle a.}的线闭环。如果如图所示，点z=i{displaystyle z=i}被认为是一个函数的极点，那么轮廓积分描述了一条围绕极点的轮廓线。这种类型的积分在复杂分析中极为常见。

第二部分 3:例子的第二部分

1. 1评估以下轮廓积分。γ{displaystyle\gamma }是沿直线连接原点和1+i{displaystyle 1+i}的曲线。∫γ(xy2+2xyi)dz{displaystyle\int _{gamma }(xy^{2}+2xyi)\mathrm {d} z}。
2. 2将轮廓线参数化。我们的曲线特别简单：x=t{displaystyle x=t}和y=t.{displaystyle y=t.}。所以我们用以下方式来写我们的轮廓。z(t)=t+it, 0≤t≤1{displaystyle z(t)=t+it,\ 0\leq t\leq 1}。
3. 3计算dzdt{displaystyle {frac {mathrm {d} z}{mathrm {d} t}}。将我们的结果代入积分。dzdt=1+i{displaystyle {frac {mathrm {d} z}{mathrm {d} t}=1+i}∫γ（xy2+2xyi）dz=∫01（t3+i2t2）（1+i）dt{displaystyle\INT _{\gamma }(xy^{2}+2xyi)\mathrm {d} z=INT _{0}^{1}(t^{3}+i2t^{2})(1+i)\mathrm {d} t} 。
4. 4评价一下。∫01(t3+i2t2)(1+i)dt=∫01(t3+i2t2+it3−2t2)dt=14+i(23+14)−23=−512+1112i{\displaystyle {\begin{aligned}\int _{0}^{1}(t^{3}+i2t^{2})(1+i)\mathrm {d} t&=int _{0}^{1}(t^{3}+i2t^{2}+it^{3}-2t^{2})\mathrm {d} t\&={\frac {1}{4}+i\left({frac {2}{3}+{frac {1}{4}}\right)-{frac {2}{3}}\&=-{\frac {5}{12}+{frac {11}{12}iend{aligned}}.
5. 5评估相同的积分，但其中γ{displaystyle \gamma }是沿y=x3{displaystyle y=x^{3}连接原点与1+i{displaystyle 1+i}的曲线。｝我们的参数化变化为x=t{displaystyle x=t}和y=t3.{displaystyle y=t^{3}。}z(t)=t+it3{displaystyle z(t)=t+it^{3}}dzdt=(1+i3t2)dt{displaystyle {\frac {mathrm {d} z}{mathrm {d} t}=(1+i3t^{2})\mathrm {d}.t}∫γ(xy2+2xyi)dz=∫01(t7+i2t4)(1+i3t2)dt=∫01(t7+i2t4+i3t9−6t6)dt=18+i(25+310)−67=−4156+710i{\displaystyle {\begin{aligned}\int _{\gamma }(xy^{2}+2xyi)\mathrm {d} z&=int _{0}^{1}(t^{7}+i2t^{4})(1+i3t^{2})\mathrm {d} t\amp;=int _{0}^{1}(t^{7}+i2t^{4}+i3t^{9}-6t^{6})\mathrm {d} t\&={\frac {1}{8}+i\left({\frac {2}{5}+{\frac {3}{10}\right)-{\frac {6}{7}\&=-{frac {41}{56}}+{frac {7}{10}}i\end{aligned}}我们在这里表明，对于非解析函数，如f(z)=xy2+2xyi,{displaystyle f(z)=xy^{2}+2xyi,}的轮廓积分取决于所选路径。我们可以通过检查实部和虚部是否满足Cauchy-Riemann方程来证明这个函数是非解析的。由于∂u∂x=y2{displaystyle {frac {partial u}{partial x}=y^{2}}和∂v∂y=2x,{displaystyle {frac {partial v}{partial y}=2x,}这足以证明非分析性。

第3部分 第3部分：轮廓积分基本定理

1. 1归纳微积分基本定理。由于该定理与等值积分有关，只要我们能找到一个反导数，就能轻松计算出等值积分的值。假设函数f(z){\displaystyle f(z)}有一个反导F(z){\displaystyle F(z)}，这样ddzF(z)=f(z){\displaystyle {frac {mathrm {d}}。}{mathrm {d} z}F(z)=f(z)}通过域D,{displaystyle D,}，让γ{\displaystyle \gamma }是D,{displaystyle D,}中的一条轮廓，其中z0{displaystyle z_{0}和z1{displaystyle z_{1}}分别是γ,{displaystyle \gamma }的起点和终点。然后∫γf(z)dz{displaystyle int _{\gamma }f(z)\mathrm {d} z}对于所有有限长度的连续路径γ{displaystyle \gamma }是独立于路径的，其值由F(z1)-F(z0).{displaystyle F(z_{1})-F(z_{0}}给出。｝
2. 2通过直接参数化来评估以下积分。γ{displaystyle \gamma }是逆时针从z=-i{displaystyle z=-i}到z=i.{displaystyle z=i.}的半圆，∫γzdz{displaystyle int _{gamma }{sqrt {z}}\mathrm {d} z}。
3. 3参数化γ,{displaystyle \gamma ,}找到dzdt,{displaystyle {frac {mathrm {d} z}{mathrm {d} t}},}并评估。z（t）=eit,-π2≤t≤π2{displaystyle z（t）=e^{it},-{frac {pi }{2}}\leq t\leq {frac {pi }{2}}dzdt=ieit{displaystyle {frac {mathrm {d} z}{mathrm {d}}=ie^{itt}}=ie^{it}}∫γzdz=∫−π/2π/2e12Log⁡eitieitdt=i∫−π/2π/2e32itdt=23e32it|−π/2π/2=23(e3π4i−e−3π4i)=232isin⁡3π4=223i{\displaystyle {\begin{aligned}\int _{\gamma }{\sqrt {z}}\mathrm {d} z&=int _{-\pi /2}^{\pi /2}e^{{frac {1}{2}}operatorname {Log} e^{it}ie^{it}\mathrm {d} t\amp;=iint _{-\pi /2}^{\pi /2}e^{{\frac {3}{2}it}mathrm {d} t\&={\frac {2}{3}e^{{\frac {3}{2}it}{Bigg |}_{-pi /2}^{\pi /2}\&={{frac {2}{3}}\left(e^{{\frac {3\pi }{4}i}-e^{-{frac {3\pi }{4}i}\right)\amp;={\frac {2}{3}2i\sin {frac {3\pi }{4}}\amp;={\frac {2{\sqrt {2}}{3}i\end{aligned}}.
4. 4用等值积分的基本定理来评估同一个积分。然而，在这种方法中，积分中的z{displaystyle {sqrt {z}}}出现了问题。因为我们知道z=e12Logz,{displaystyle {sqrt {z}}=e^{{frac {1}{2}}operatorname {Log} z},}对数函数的存在表明有一个分支切口，我们不能进行积分。幸运的是，我们可以选择我们的分支切割，使我们的轮廓在我们的领域中得到良好的定义。在这种情况下，对数的主分支，即分支切口由非正实数组成，是可行的，因为我们的轮廓线会绕过该分支切口。只要我们认识到主对数有一个定义在(-π,π],{displaystyle (-π\pi ,\pi ],}上的参数，剩下的步骤就是简单的计算。∫γzdz=23z3/2|-ii=23(i32-(-i)32)=23(e32Logi-e32Log(-i)){\displaystyle {\begin{aligned}int _{\gamma }{\sqrt {z}\mathrm {d} z&={\frac {2}{3}}z^{3/2}{Bigg |}_{-i}^{i}\&={frac {2}{3}}\left(i^{\frac {3}{2}-(-i)^{frac {3}{2}\right)\amp;={\frac {2}{3}}\left(e^{{\frac {3}{2}}\operatorname {Log} i}-e^{{\frac {3}{2}}\operatorname {Log｝(-i)}\right)end{aligned}}对于对数的主分支，我们看到Logi=iπ2{displaystyle\operatorname {Log} i=i{frac {pi }{2}}，而Log(-i)=-iπ2.{displaystyle\operatorname {Log}}。(-i)=-i{frac {\pi }{2}}。}∫γzdz=23(e32iπ2-e-32iπ2)=23(e3π4i-e-3π4i)=232isin3π4=223i{displaystyle {begin{aligned}int _{\gamma }{sqrt {z}\mathrm {d} z&={\frac {2}{3}}\left(e^{{\frac {3}{2}}i{frac {pi }{2}}-e^{-{frac {3}{2}}i{frac {pi }{2}}}\right)\amp;={{frac {2}{3}}\left(e^{{\frac {3\pi }{4}i}-e^{-{frac {3\pi }{4}i}\right)\amp;={\frac {2}{3}2i\sin {frac {3\pi }{4}}\amp;={\frac {2{\sqrt {2}}{3}i\end{aligned}}.

提示