决定股票价格

就任何可交易资产的准确定价达成一致具有挑战性，这就是股价不断变化的原因。事实上，公司几乎每天都不会改变估值，但它们的股价和估值几乎每秒钟都在变化。就任何可交易资产的正确定价达成共识的困难导致了短期套利机会。

但许多成功的投资归根结底是一个简单的问题，即当前的估值——对于预期的未来回报，当前的正确价格是多少？

关键要点

• 二项期权定价模型采用迭代方法，利用多周期法对美国期权进行价值评估。
• 在这个模型中，每次迭代都有两种可能的结果，一种是沿着二叉树向上移动，一种是向下移动。
• 与著名的Black-Scholes模型相比，该模型更直观，在实际应用中更为频繁。

二元期权估值

在竞争市场中，为了避免套利机会，具有相同回报结构的资产必须具有相同的价格。期权的估值一直是一项具有挑战性的任务，定价的变化会带来套利机会。Black-Scholes仍然是最流行的期权定价模型之一，但有其局限性。

二项式期权定价模型是另一种常用的期权定价方法。

示例

假设某一股票有一个当前市价为100美元的看涨期权，ATM期权的执行价为100美元，有效期为一年。有两位交易员，彼得和保拉，他们都同意股价在一年内要么涨到110美元，要么跌到90美元。

他们同意在一年的时间内预期价格水平，但对上下移动的可能性不一致。彼得认为，该股价格升至110美元的概率为60%，而保拉则认为这是40%。

基于此，谁愿意为看涨期权付出更多的代价？可能是彼得，因为他预计上升的可能性很大。

二项式期权计算

估值所依赖的两种资产是看涨期权和标的股票。与会者一致认为，标的股价一年内可以从目前的100美元转为110美元或90美元，没有其他价格变动的可能。

在一个无套利的世界里，如果你必须创建一个由这两种资产组成的投资组合，即看涨期权和标的股票，这样无论标的价格是110美元还是90美元，投资组合的净回报总是保持不变。假设你购买了“d”股的基础和短期一个看涨期权来创建这个投资组合。

如果价格涨到110美元，你的股票价值110美元，你将损失10美元。你的投资组合净值将是（110d-10）。

如果价格降到90美元，你的股票将价值90美元，期权将毫无价值地到期。你的投资组合净值将是（90天）。

如果你想让你的投资组合的价值保持不变，不管潜在的股价走势如何，那么你的投资组合价值在任何一种情况下都应该保持不变：

小时（天）−m=升（d）where:h=Highest 潜在潜在定价=潜在股票数量SM=短期买入损失金额PAYFFL=最低潜在潜在价格\begin{aligned}&amp；h（d）-m=l（d）\\&amp\textbf{其中：}\\&amp；h=\text{最高潜在基础价格}\\&amp；d=\text{标的股份数}\\&amp；m=\text{短期赎回赔付损失的金额}\\&amp；l=\text{最低潜在基础价格}\\\end{对齐}​小时（天）−m=升（d）where:h=Highest 潜在潜在价格=潜在股票数量M=短期赎回赔付损失金额L=最低潜在价格​

因此，如果你购买了一半的股份，假设可以进行部分购买，你将设法创建一个投资组合，使其价值在给定的一年时间框架内，在两个可能的州保持不变。

110天−10=90dd=12\begin{aligned}&amp；110d-10=90d\\&amp；d=\frac{1}{2}\\\ end{aligned}​110天−10=90dd=21​​

这个投资组合的价值，用（90d）或（110d-10）=45表示，是一年下来的线。为计算其现值，可按无风险收益率（假设为5%）折现。

现值=90d×电子(−5%×1年）=45×0.9523=42.85\开始{对齐}\文本{现值}&amp；=90d\times e^{（-5\%\times 1\text{Year}）}\\&amp；=45\乘以0.9523\\&amp；=42.85\\\结束{对齐}现值​=90天×电子(−5%×1年）=45×0.9523=42.85​

目前，投资组合包括½ 标的股票份额（市价100美元）和一次短期认购，应等于现值。

12×100−1×买入价=$42.85买入价=$7.14，即今天的买入价\begin{aligned}&amp\frac{1}{2}\times 100-1\times\text{Call Price}=\$42.85\\&amp\text{Call Price}=\$7.14\text{，即今天的买入价}\\\end{aligned}​21​×100−1×买入价=$42.85买入价=$7.14，即今天的买入价​

由于这是基于这样一个假设，即无论基础价格以何种方式变动，投资组合价值都保持不变，因此上涨或下跌的概率不起任何作用。无论基础价格变动如何，投资组合都保持无风险。

在这两种情况下（假设上升到110美元，下降到90美元），你的投资组合是中性的风险和赚取无风险的回报率。

因此，两位交易员彼得和保拉都愿意为这一看涨期权支付相同的7.14美元，尽管他们对上涨概率的看法不同（60%和40%）。他们个人感知的概率在期权估价中并不重要。

相反，假设个体的概率很重要，套利机会可能已经出现了。在现实世界中，这样的套利机会存在着微小的价差，并在短期内消失。

但在所有这些计算中被大肆炒作的波动性在哪里呢？波动性是影响期权定价的一个重要而敏感的因素？

波动性已经包含在问题定义的性质中。假设价格水平（110美元和90美元）的两种状态（也就是只有两种，因此称为“二项式”）的话，波动性就隐含在这个假设中，并且自动包含（本例中以10%的方式）。

布莱克斯科尔斯

但这种方法是否正确，是否与常用的Black-Scholes定价方法一致？选项计算器结果（由OIC提供）与计算值非常匹配：

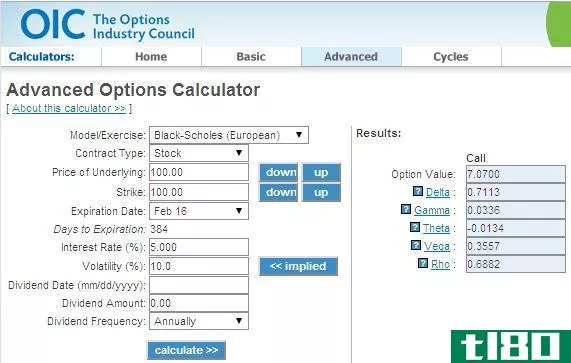
不幸的是，现实世界并不像“只有两个州”那么简单。股票在到期前可以达到好几个价格水平。

有没有可能将所有这些多个层次都包含在一个仅限于两个层次的二项式定价模型中？是的，这是很有可能的，但要理解它需要一些简单的数学。

简单数学

概括这个问题和解决方案：

“X”是股票的当前市场价格，“X*u”和“X*d”是“t”年后涨跌的未来价格。因子“u”将大于1，因为它表示向上移动，“d”将位于0和1之间。对于上述示例，u=1.1，d=0.9。

看涨期权的收益是“Pup”和“Pdn”，用于到期时的上下波动。

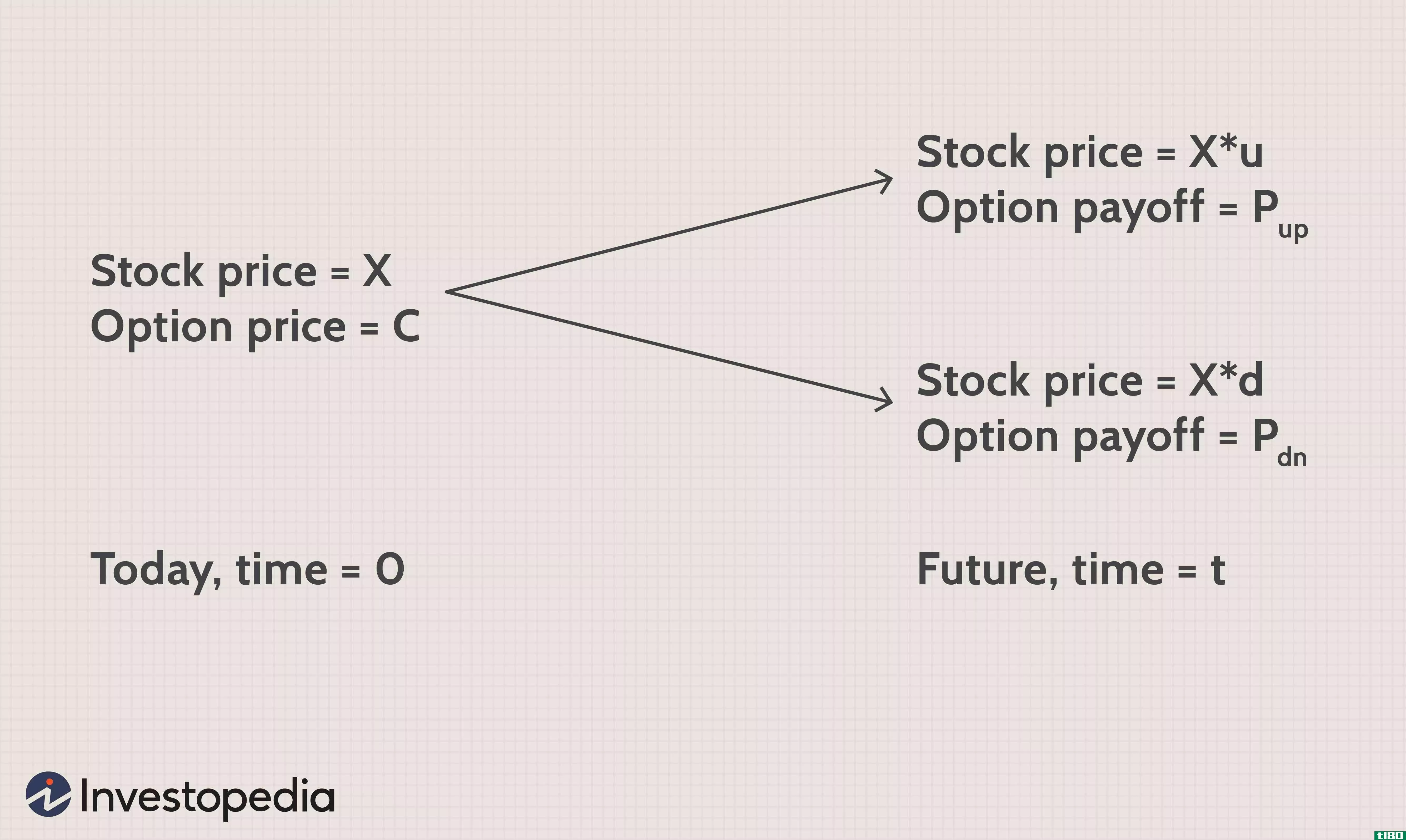
如果你建立一个由今天购买的“s”股和做空一个看涨期权组成的投资组合，那么在时间“t”之后：

VUM=秒×十×u−Pupwhere:VUM=Value 向上移动时的投资组合\begin{aligned}&amp\text{VUM}=s\times X\times u-P\text{up}\\&amp\textbf{其中：}\\&amp\text{VUM}=\text{上移时投资组合的值}\\\结束{对齐}​VUM=秒×十×u−小狗​where:VUM=Value 投资组合上升时​

VDM=秒×十×d−Pdownwhere:VDM=Value 下移时的投资组合\begin{aligned}&amp\text{VDM}=s\times X\times d-P\text{down}\\&amp\textbf{其中：}\\&amp\text{VDM}=\text{下移时投资组合的值}\\\结束{对齐}​VDM=秒×十×d−Pdown公司​where:VDM=Value 在下跌的情况下投资组合的​

对于任何一种价格变动情况下的类似估值：

s×十×u−小狗=s×十×d−Pdowns\times X\times u-P\uText{up}=s\times X\times d-P\uText{down}s×十×u−小狗​=s×十×d−Pdown公司​

s=小狗−PdownX公司×(u−d） =要购买的股票数量=无风险投资组合\begin{aligned}s&amp；=\frac{P\uText{up}-P\uText{down}}{X\times（u-d）}\\&amp；=\text{购买股份的数量}\\&amp\幻影{=}\text{无风险投资组合}\\\end{aligned}s​=十×(u−d） 小狗​−Pdown公司​​=购买股票的数量=无风险投资组合​

在“t”年末，投资组合的未来价值为：

上移时=s×十×u−Pup=小狗−普多努−d×u−Pup\begin{aligned}\text{上移时}&amp；=s\times X\times u-P\utext{up}\\&amp=\向上移动时的frac{P\uText{up}-P\uText{down}}{u-d}\times u-P\uText{up}\\\ end{aligned}​=s×十×u−小狗​=u−dPup公司​−Pdown公司​​×u−小狗​​

下移时=s×十×d−Pdown=小狗−普多努−d×d−Pdown\begin{aligned}\text{下移时}&amp；=s\times X\times d-P\text{down}\\&amp=\向下移动时的frac{P\uText{up}-P\uText{down}}{u-d}\times d-P\uText{down}\\\ end{aligned}​=s×十×d−Pdown公司​=u−dPup公司​−Pdown公司​​×d−Pdown公司​​

现值可以用无风险收益率折现：

PV=e(−（右）×[小狗−普多努−d×u−小狗]where:PV=Present-Day Valuer=返回率=时间，单位为年\begin{aligned}&amp\text{PV}=e（-rt）\times\left[\frac{P\u\ text{up}-P\text{down}}{u-d}\times u-P\text{up}\right]\\ amp\textbf{其中：}\\&amp\text{PV}=\text{Present Day Value}\\&amp；r=\text{return}\\&amp；t=\text{Time，单位为年}\\\end{aligned}​PV=e(−（右）×[u−dPup公司​−Pdown公司​​×u−小狗​]where:PV=Present-Day Valuer=返回率=时间（以年为单位）​

这应与以X价格持有“s”股的投资组合相匹配，短期买入价值“c”（目前持有的（s*X-c）应等同于此计算）。求解“c”最终得出：

注意：如果看涨期权溢价被做空，它应该是投资组合的加法，而不是减法。

c=e(−rt）u−d×[(电子(−（右）−（d）×蛹+（u−电子(−rt））×Pdown]c=\frac{e（-rt）}{u-d}\times[（e（-rt）-d）\times P\u\ text{up}+（u-e（-rt））\times P\u\ text{down}]c=u−数据元素(−（右）​×[(电子(−（右）−（d）×小狗​+(u−电子(−rt））×Pdown公司​]

另一种写公式的方法是重新排列：

取“q”为：

q=e(−（右）−杜−dq=\frac{e（-rt）-d}{u-d}q=u−数据元素(−（右）−d​

然后方程变成：

c=e(−（右）×(q×小狗+（1）−问）×Pdown）c=e（-rt）\times（q\times P\uText{up}+（1-q）\times P\uText{down}）c=e(−（右）×(q×小狗​+(1−问）×Pdown公司​)

用“q”重新排列方程提供了一个新的视角。

现在，您可以将“q”解释为底层向上移动的概率（因为“q”与Pup相关，“1-q”与Pdn相关）。总的来说，这个公式代表了当前的期权价格，即到期收益的折现值。

这个“q”是不同的

这个概率“q”与基础货币的上移或下移的概率有何不同？

VSP=q×十×u+（1）−问）×十×dwhere:VSP=Value 时间t\begin{aligned}&amp；的股价\text{VSP}=q\times X\times u+（1-q）\times X\times d\\&amp\textbf{其中：}\\&amp\text{VSP}=\text{Time的股价值}t\\\end{aligned}​VSP=q×十×u+（1）−问）×十×dwhere:VSP=Value 时间t的股价​

替换“q”的值并重新排列，时间“t”的股价为：

股票价格=e（rt）×X\开始{对齐}&amp\text{Stock Price}=e（rt）\times X\\\end{aligned}​股票价格=e（rt）×十​

在这两个国家的假设世界中，股价仅仅是以无风险回报率来上涨，就像一种无风险资产，因此它仍然独立于任何风险。在这种模型下，投资者对风险漠不关心，因此构成了风险中性模型。

概率“q”和“（1-q）”称为风险中性概率，估值方法称为风险中性估值模型。

示例场景有一个重要的要求——未来的回报结构需要精确（级别110美元和90美元）。在现实生活中，这样清晰的阶梯式价格水平是不可能的；相反，价格是随机波动的，可能会在多个层次上结算。

为了进一步扩展示例，假设两步价格水平是可能的。我们知道第二步的最终收益，我们需要在今天对期权进行估值（在第一步）：

反向操作，中间第一步估值（t=1）可以使用第二步（t=2）的最终收益进行，然后使用这些计算出的第一步估值（t=1），可以通过这些计算得出当前估值（t=0）。

为了得到第二位的期权定价，使用了第四位和第五位的收益。为了得到第三个的定价，使用了第五个和第六个的收益。最后，计算出的2和3的收益被用来得到1的定价。

请注意，此示例假定两个步骤的向上（和向下）移动的系数相同–u和d以复合方式应用。

一个有效的例子

假设一个执行价为110美元的看跌期权目前的价格为100美元，一年后到期。年无风险率为5%。价格预计每半年上涨20%，下跌15%。

这里，u=1.2，d=0.85，x=100，t=0.5

利用上述导出的

q=e(−（右）−杜−dq=\frac{e（-rt）-d}{u-d}q=u−数据元素(−（右）−d​

我们得到q=0.35802832

看跌期权在第2点的价值，

p2=e(−（右）×(p×Pupup+（1）−q） 蛹（DN）where:p=Price 看跌期权的\开始{对齐}&amp；p\u 2=e（-rt）\times（p\times p\text{upup}+（1-q）p\text{updn}）\\&amp\textbf{其中：}\\&amp；p=\text{看跌期权价格}\\\结束{对齐}​第2页​=电子(−（右）×(p×化蛹​+(1−q） 蛹​)where:p=Price 看跌期权的价值​

在Pupup条件下，基础将为=100*1.2*1.2=$144，导致Pupup=0

在Pupdn条件下，基础将是=100*1.2*0.85=$102导致Pupdn=$8

在Pdndn条件下，基础将=100*0.85*0.85=$72.25导致Pdndn=$37.75

p2=0.975309912*（0.35802832*0+（1-0.35802832）*8）=5.008970741

同样，p3=0.975309912*（0.35802832*8+（1-0.35802832）*37.75）=26.42958924

p1=e(−（右）×(q×p2+（1）−q） p3）pU1=e（-rt）\times（q\乘以pU2+（1-q）pU3）p1​=电子(−（右）×(q×第2页​+(1−q） p3页​)

因此，看跌期权的价值，p1=0.975309912*（0.35802832*5.008970741+（1-0.35802832）*26.42958924）=18.29美元。

类似地，二项式模型允许您打破整个选项持续时间，以进一步细化多个步骤和级别。使用计算机程序或电子表格，您可以一次向后工作一步，以获得所需选项的当前值。

另一个例子

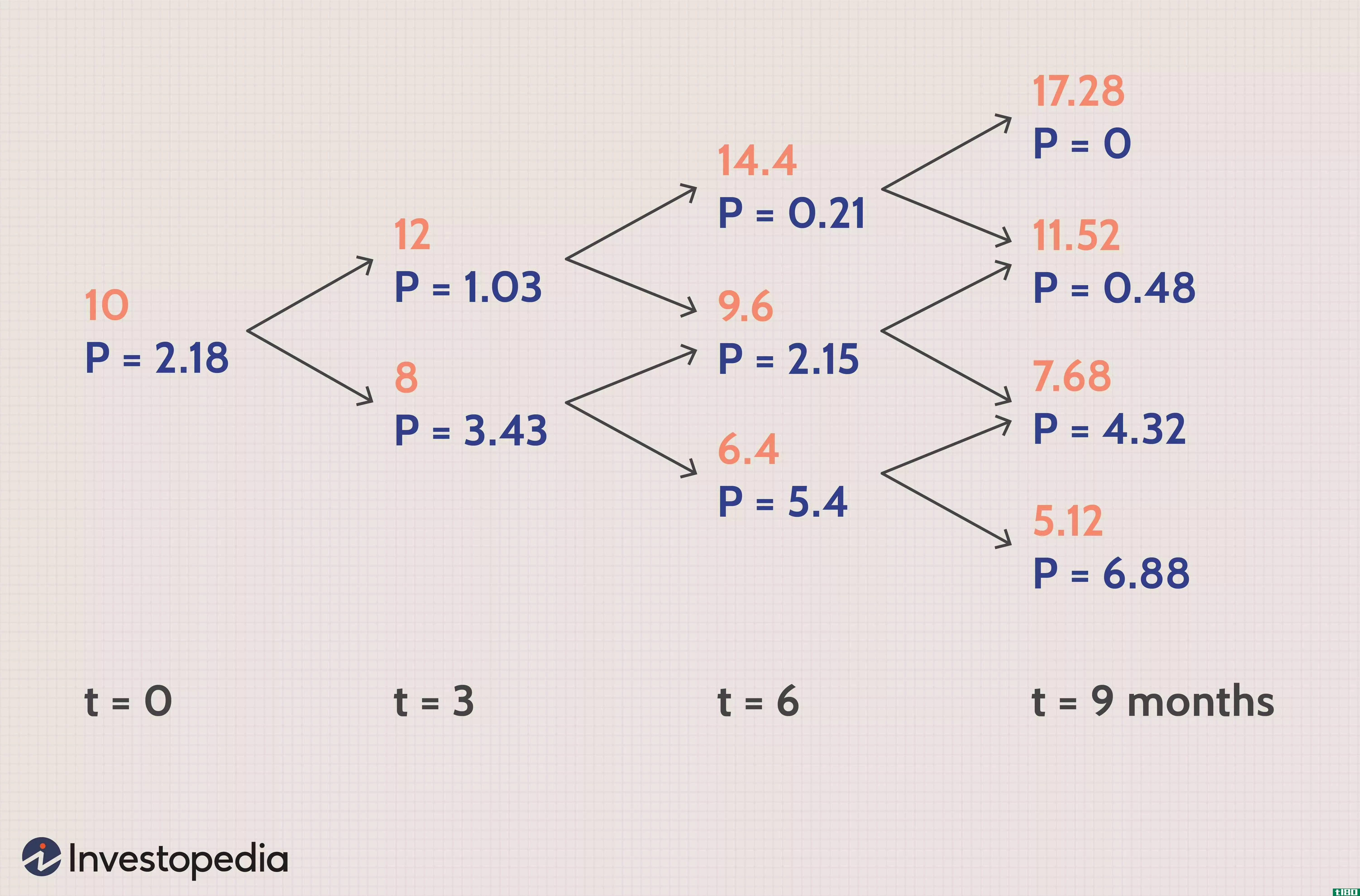
假设欧式看跌期权有效期为9个月，执行价为12美元，当前基础价格为10美元。假设所有期间的无风险利率为5%。假设每三个月，基础价格可以向上或向下移动20%，得到u=1.2，d=0.8，t=0.25和一个三步二叉树。

红色表示基础价格，蓝色表示看跌期权的收益。

风险中性概率“q”计算为0.531446。

使用上述“q”值和t=9个月时的收益值，t=6个月时的相应值计算如下：

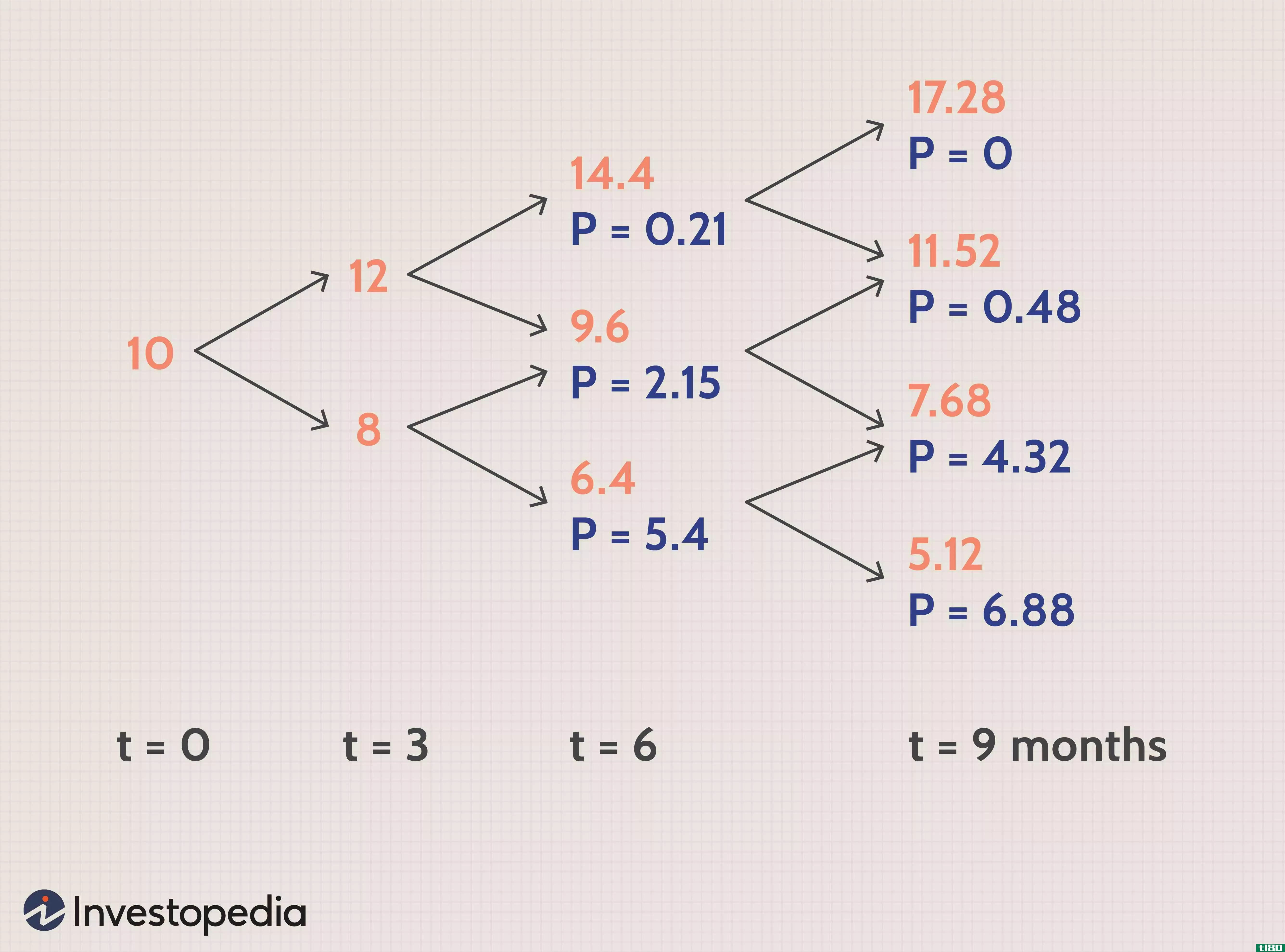
此外，使用t=6时的这些计算值，t=3时的值和t=0时的值为：

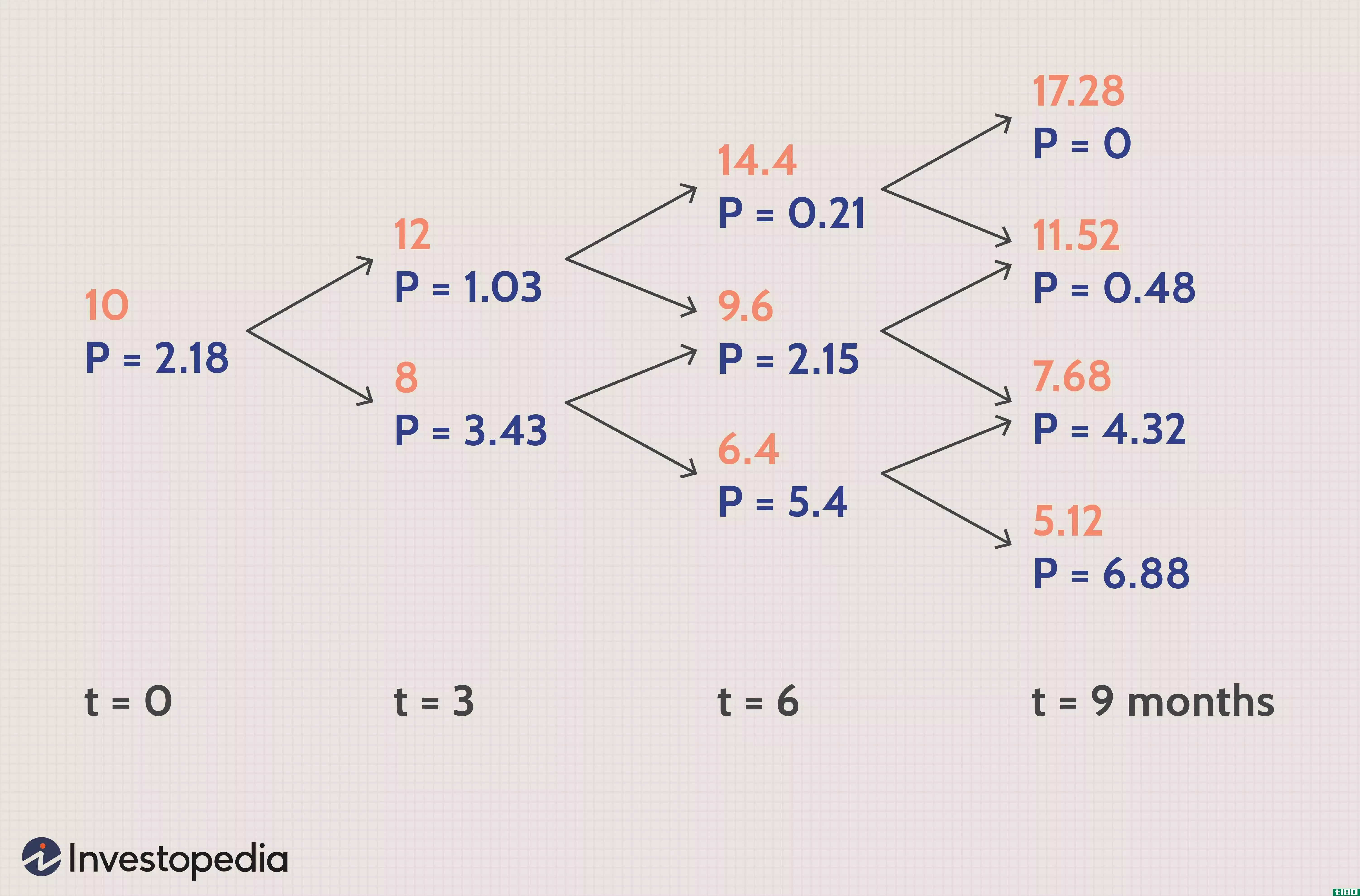
这使得看跌期权的当前价值为2.18美元，非常接近使用布莱克-斯科尔斯模型（Black-Scholes model，2.30美元）计算的结果。

底线

虽然使用计算机程序可以使这些密集的计算变得容易，但对未来价格的预测仍然是二项式期权定价模型的一个主要局限。时间间隔越细，就越难以高精度地预测每个周期结束时的收益。

然而，灵活地纳入不同时期的预期变化是一个优势，这使得它适合于美式期权定价，包括早期行使估值。

使用二项式模型计算的值与其他常用模型（如Black-Scholes）计算的值非常接近，这表明了二项式模型在期权定价中的实用性和准确性。二项式定价模型可以根据交易者的偏好进行开发，可以作为Black-Scholes的替代品。